How to Draw Planar Analysis

Molecular Shape

The Shape of Molecules

    The three dimensional shape or configuration of a molecule is an of import feature. This shape is dependent on the preferred spatial orientation of covalent bonds to atoms having two or more bonding partners. Three dimensional configurations are best viewed with the aid of models. In order to represent such configurations on a two-dimensional surface (paper, blackboard or screen), we oftentimes use perspective drawings in which the management of a bond is specified by the line connecting the bonded atoms. 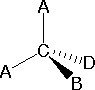In well-nigh cases the focus of configuration is a carbon atom and so the lines specifying bond directions will originate there. As defined in the diagram on the right, a uncomplicated directly line represents a bond lying approximately in the surface plane. The two bonds to substituents A in the structure on the left are of this kind. A wedge shaped bond is directed in front of this plane (thick cease toward the viewer), every bit shown by the bond to substituent B; and a hatched bond is directed in back of the plane (away from the viewer), equally shown by the bond to substituent D. Some texts and other sources may use a dashed bond in the aforementioned manner as we have divers the hatched bond, simply this can be disruptive because the dashed bond is often used to represent a partial bond (i.e. a covalent bond that is partially formed or partially broken). The post-obit examples brand use of this notation, and also illustrate the importance of including non-bonding valence shell electron pairs (colored blue) when viewing such configurations .

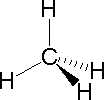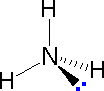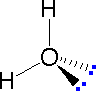Methane		Ammonia		Water

Bonding configurations are readily predicted by valence-crush electron-pair repulsion theory, commonly referred to as VSEPR in virtually introductory chemistry texts. This simple model is based on the fact that electrons repel each other, and that it is reasonable to expect that the bonds and non-bonding valence electron pairs associated with a given cantlet will prefer to exist as far apart as possible. The bonding configurations of carbon are like shooting fish in a barrel to remember, since there are only three categories.

Configuration	Bonding Partners	Bond Angles	Case
Tetrahedral	4	109.5º
Trigonal	three	120º
Linear	ii	180º

In the three examples shown above, the central cantlet (carbon) does not accept any non-bonding valence electrons; consequently the configuration may exist estimated from the number of bonding partners alone. For molecules of water and ammonia, however, the non-bonding electrons must be included in the calculation. In each case there are four regions of electron density associated with the valence shell so that a tetrahedral bond angle is expected. The measured bond angles of these compounds (H₂O 104.5º & NH_iii 107.3º) show that they are closer to being tetrahedral than trigonal or linear. Of form, it is the configuration of atoms (not electrons) that defines the the shape of a molecule, and in this sense ammonia is said to exist pyramidal (non tetrahedral). The compound boron trifluoride, BF₃, does non take non-bonding valence electrons and the configuration of its atoms is trigonal. Dainty treatments of VSEPR theory accept been provided past Oxford and Purdue . Click on the university proper name to visit their site.

The best fashion to written report the iii-dimensional shapes of molecules is by using molecular models. Many kinds of model kits are available to students and professional chemists. Some of the useful features of concrete models can exist approximated by the model viewing applet Jmol. This powerful visualization tool allows the user to motility a molecular stucture in any way desired. Atom distances and angles are easily determined. To measure a distance, double-click on 2 atoms. To measure a bail angle, practice a double-click, unmarried-click, double-click on 3 atoms. To measure a torsion angle, do a double-click, single-click, single-click, double-click on 4 atoms. A popular-up menu of commands may be accessed by the correct push on a PC or a control-click on a Mac while the cursor is inside the display frame.
You may examine several Jmol models of compounds discussed above by .

One way in which the shapes of molecules manifest themselves experimentally is through molecular dipole moments. A molecule which has one or more than polar covalent bonds may have a dipole moment as a issue of the accumulated bond dipoles. In the case of h2o, nosotros know that the O-H covalent bond is polar, due to the different electronegativities of hydrogen and oxygen. Since there are two O-H bonds in water, their bond dipoles will interact and may event in a molecular dipole which tin exist measured. The following diagram shows four possible orientations of the O-H bonds.

The bail dipoles are colored magenta and the resulting molecular dipole is colored blue. In the linear configuration (bond bending 180º) the bond dipoles cancel, and the molecular dipole is zero. For other bond angles (120 to 90º) the molecular dipole would vary in size, being largest for the 90º configuration. In a similar manner the configurations of methyl hydride (CH₄) and carbon dioxide (CO₂) may exist deduced from their zip molecular dipole moments. Since the bail dipoles have canceled, the configurations of these molecules must exist tetrahedral (or foursquare-planar) and linear respectively.
The case of methane provides insight to other arguments that have been used to confirm its tetrahedral configuration. For purposes of discussion we shall consider three other configurations for CH₄, square-planar, square-pyramidal and triangular-pyramidal.
Models of these possibilities may be examined past .

Substitution of one hydrogen by a chlorine atom gives a CH₃Cl compound. Since the tetrahedral, foursquare-planar and square-pyramidal configurations have structurally equivalent hydrogen atoms, they would each give a unmarried substitution product. However, in the trigonal-pyramidal configuration one hydrogen (the noon) is structurally different from the other iii (the pyramid base of operations). Substitution in this instance should give ii different CH₃Cl compounds if all the hydrogens react. In the case of disubstitution, the tetrahedral configuration of methane would lead to a unmarried CH₂Cl₂ product, but the other configurations would requite two different CH₂Cl₂ compounds. These substitution possibilities are shown in the above insert.

Isomers

Isomers

Structural Formulas
Information technology is necessary to draw structural formulas for organic compounds because in near cases a molecular formula does not uniquely represent a unmarried compound. Unlike compounds having the same molecular formula are called isomers, and the prevalence of organic isomers reflects the boggling versatility of carbon in forming strong bonds to itself and to other elements.
When the group of atoms that make up the molecules of dissimilar isomers are bonded together in fundamentally dissimilar ways, we refer to such compounds equally constitutional isomers. There are seven ramble isomers of C_ivH₁₀O, and structural formulas for these are drawn in the following table. These formulas represent all known and possible C_fourH₁₀O compounds, and display a common structural feature. There are no double or triple bonds and no rings in any of these structures.. Note that each of the carbon atoms is bonded to four other atoms, and is saturated with bonding partners.

Structural Formulas for C₄H_xO Isomers

Kekulé Formula	Condensed Formula	Shorthand Formula

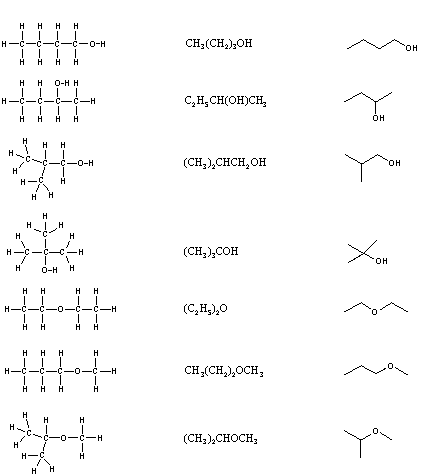Simplification of structural formulas may be achieved without any loss of the information they convey. In condensed structural formulas the bonds to each carbon are omitted, but each distinct structural unit (group) is written with subscript numbers designating multiple substituents, including the hydrogens. Shorthand (line) formulas omit the symbols for carbon and hydrogen entirely. Each straight line segment represents a bond, the ends and intersections of the lines are carbon atoms, and the correct number of hydrogens is calculated from the tetravalency of carbon. Non-bonding valence beat electrons are omitted in these formulas.
Developing the power to visualize a three-dimensional construction from two-dimensional formulas requires do, and in most cases the assist of molecular models. Equally noted earlier, many kinds of model kits are available to students and professional chemists, and the beginning student is encouraged to obtain one.

Constitutional isomers have the aforementioned molecular formula, but their concrete and chemic backdrop may exist very different. For an example Click Here.

Distinguishing Carbon Atoms
When discussing structural formulas, it is often useful to distinguish unlike groups of carbon atoms past their structural characteristics. A chief carbon (1º) is ane that is bonded to no more than one other carbon atom. A secondary carbon (2º) is bonded to 2 other carbon atoms, and tertiary (3º) and quaternary (4º) carbon atoms are bonded respectively to iii and iv other carbons. The three C_vH₁₂ isomers shown beneath illustrate these terms.

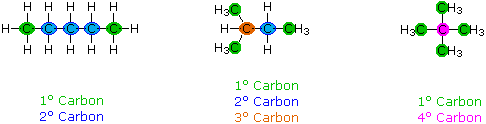
Structural differences may occur within these four groups, depending on the molecular constitution. In the formula on the right all four 1º-carbons are structurally equivalent (retrieve the tetrahedral configuration of tetravalent carbon); all the same the key formula has two equivalent 1º-carbons (bonded to the 3º carbon on the left terminate) and a unmarried, structurally different 1º-carbon (bonded to the 2º-carbon) at the right end. Similarly, the left-near formula has two structurally equivalent 2º-carbons (side by side to the ends of the chain), and a structurally dissimilar 2º-carbon in the eye of the chain. A consideration of molecular symmetry helps to distinguish structurally equivalent from nonequivalent atoms and groups. The power to distinguish structural differences of this kind is an essential role of mastering organic chemistry. It will come with practice and feel.

Our ability to draw structural formulas for molecules is remarkable. To run into how this is done Click Here.

Formula Analysis

Analysis of Molecular Formulas

Although structural formulas are essential to the unique description of organic compounds, it is interesting and instructive to evaluate the information that may be obtained from a molecular formula lonely. Three useful rules may exist listed:

1. The number of hydrogen atoms that can be bonded to a given number of carbon atoms is limited by the valence of carbon. For compounds of carbon and hydrogen (hydrocarbons) the maximum number of hydrogen atoms that can be bonded to n carbons is 2n + 2 (n is an integer). In the case of methane, CH₄, n=1 & 2n + 2 = iv. The origin of this formula is axiomatic past because a hydrocarbon fabricated up of a chain of carbon atoms. Hither the middle carbons volition each have two hydrogens and the two finish carbons have three hydrogens each. Thus, a vi-carbon chain (n = 6) may be written H-(CH₂)₆-H, and the full hydrogen count is (2 10 6) + 2 = 14. The presence of oxygen (valence = two) does non change this relationship, so the previously described C₄H_tenO isomers follow the rule, north=iv & 2n + 2 = 10. Halogen atoms (valence = 1) should be counted equivalent to hydrogen, as illustrated by C₃H₅Cl₃, northward = 3 & 2n + 2 = 8 = (5 + 3). If nitrogen is present, each nitrogen cantlet (valence = 3) increases the maximum number of hydrogens by one.
   

   Some Plausible Molecular Formulas	C7H16O3, C9H18, C15H28Oiii, C6HxviNii
   Some Impossible Molecular Formulas	C8H20Ohalf-dozen, C23Hfifty, C5HtenCl4, C4H12NO

   
   
2. For stable organic compounds the full number of odd-valenced atoms is fifty-fifty. Thus, when even-valenced atoms such as carbon and oxygen are bonded together in any number and in whatever manner, the number of remaining unoccupied bonding sites must be even. If these sites are occupied past univalent atoms such equally H, F, Cl, etc. their total number will necessarily exist fifty-fifty. Nitrogen is too an odd-valenced atom (3), and if it occupies a bonding site on carbon it adds two additional bonding sites, thus maintaining the even/odd parity.
   

   Some Plausible Molecular Formulas	C4H4Cl2, C5HnineOBr, CfiveH11NOii, C12H18N2FCl
   Some Impossible Molecular Formulas	CfiveH9O2, C4HvClBr, C6H11NtwoO, CxH18NCl2

   
   
3. The number of hydrogen atoms in stable compounds of carbon, hydrogen & oxygen reflects the number of double bonds and rings in their structural formulas. Consider a hydrocarbon with a molecular structure consisting of a unproblematic concatenation of four carbon atoms, CH₃CH_iiCH₂CH_iii. The molecular formula is C_ivH₁₀ (the maximum number of bonded hydrogens by the 2n + 2 rule). If the four carbon atoms form a ring, two hydrogens must be lost. Similarly, the introduction of a double bond entails the loss of two hydrogens, and a triple bond the loss of four hydrogens.

   

   From the above give-and-take and examples it should exist clear that the molecular formula of a hydrocarbon (C_nH_m) provides information about the number of rings and/or double bonds that must be present in its structural formula. Past rule #2 m must be an fifty-fifty number, so if m < (2n + 2) the difference is also an even number that reflects whatever rings and double bonds. A triple bail is counted as two double bonds.

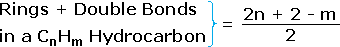
   The presence of ane or more than nitrogen atoms or halogen substituents requires a modified analysis. The above formula may be extended to such compounds by a few simple principles:

   • The presence of oxygen does non alter the relationship.
   • All halogens present in the molecular formula must be replaced by hydrogen.
   • Each nitrogen in the formula must be replaced by a CH moiety.

Resonance

Resonance

Kekulé structural formulas are essential tools for understanding organic chemistry. However, the structures of some compounds and ions cannot be represented by a single formula. For case, sulfur dioxide (And then_ii) and nitric acrid (HNO₃) may each be described by two equivalent formulas (equations 1 & 2). For clarity the 2 cryptic bonds to oxygen are given different colors in these formulas.

1) sulfur dioxide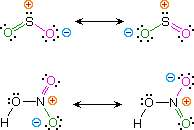
2) nitric acid

If but one formula for sulfur dioxide was correct and accurate, then the double bond to oxygen would be shorter and stronger than the single bond. Since experimental evidence indicates that this molecule is bent (bond angle 120º) and has equal length sulfur : oxygen bonds (i.432 Å), a single formula is inadequate, and the actual structure resembles an average of the two formulas. This averaging of electron distribution over two or more hypothetical contributing structures (approved forms) to produce a hybrid electronic structure is chosen resonance. Likewise, the structure of nitric acid is best described as a resonance hybrid of two structures, the double headed arrow being the unique symbol for resonance.

The above examples represent one extreme in the awarding of resonance. Here, ii structurally and energetically equivalent electronic structures for a stable compound can be written, but no single construction provides an authentic or even an adequate representation of the true molecule. In cases such as these, the electron delocalization described by resonance enhances the stability of the molecules, and compounds or ions composed of such molecules often evidence exceptional stability.

3) formaldehyde

The electronic structures of well-nigh covalent compounds do non suffer the inadequacy noted above. Thus, completely satisfactory Kekulé formulas may be drawn for water (H₂O), methane (CH₄) and acetylene C_iiH_ii). Nevertheless, the principles of resonance are very useful in rationalizing the chemical behavior of many such compounds. For example, the carbonyl grouping of formaldehyde (the carbon-oxygen double bond) reacts readily to requite addition products. The course of these reactions can be explained by a small contribution of a dipolar resonance contributor, equally shown in equation 3. Hither, the showtime contributor (on the left) is clearly the best representation of this molecular unit, since there is no charge separation and both the carbon and oxygen atoms accept accomplished valence shell neon-similar configurations by covalent electron sharing. If the double bail is broken heterolytically, formal charge pairs result, every bit shown in the other ii structures. The preferred charge distribution will have the positive charge on the less electronegative atom (carbon) and the negative accuse on the more electronegative atom (oxygen). Therefore the middle formula represents a more reasonable and stable construction than the one on the correct. The application of resonance to this case requires a weighted averaging of these canonical structures. The double bonded structure is regarded every bit the major contributor, the heart structure a minor contributor and the right hand structure a not-contributor. Since the centre, charge-separated contributor has an electron scarce carbon atom, this explains the tendency of electron donors (nucleophiles) to bail at this site.

The basic principles of the resonance method may now exist summarized.
For a given chemical compound, a fix of Lewis / Kekulé structures are written, keeping the relative positions of all the component atoms the aforementioned. These are the canonical forms to be considered, and all must have the aforementioned number of paired and unpaired electrons.
The post-obit factors are important in evaluating the contribution each of these approved structures makes to the actual molecule.

1. The number of covalent bonds in a structure. (The greater the bonding, the more of import and stable the contributing structure.)
2. Formal charge separation. (Other factors bated, accuse separation decreases the stability and importance of the contributing structure.)
3. Electronegativity of charge begetting atoms and charge density. (High charge density is destabilizing. Positive charge is best accommodated on atoms of depression electronegativity, and negative charge on high electronegative atoms.)

The stability of a resonance hybrid is always greater than the stability of any approved contributor. Consequently, if 1 canonical grade has a much greater stability than all others, the hybrid volition closely resemble it electronically and energetically. This is the example for the carbonyl group (eq.3). The left hand C=O construction has much greater total bonding than either accuse-separated structure, so it describes this functional grouping rather well. On the other hand, if two or more canonical forms take identical low energy structures, the resonance hybrid volition have exceptional stabilization and unique properties. This is the case for sulfur dioxide (eq.ane) and nitric acid (eq.2).

4) carbon monoxide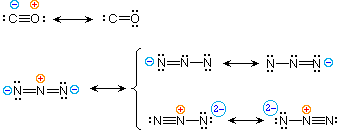
5) azide anion

To illustrate these principles we shall consider carbon monoxide (eq.4) and azide anion (eq.5). In each instance the most stable canonical form is on the left. For carbon monoxide, the additional bonding is more important than charge separation. Furthermore, the double bonded structure has an electron scarce carbon atom (valence crush sextet). A similar destabilizing cistron is nowadays in the two azide canonical forms on the height row of the bracket (3 bonds vs. iv bonds in the left virtually construction). The bottom row pair of structures take 4 bonds, but are destabilized by the high charge density on a single nitrogen atom.

All the examples on this page demonstrate an important restriction that must exist remembered when using resonance. No atoms change their positions inside the common structural framework. Only electrons are moved.

Orbitals

Diminutive and Molecular Orbitals

A more than detailed model of covalent bonding requires a consideration of valence trounce atomic orbitals. For second period elements such as carbon, nitrogen and oxygen, these orbitals accept been designated 2_south, 2p_x, 2p_y & 2p_z. The spatial distribution of electrons occupying each of these orbitals is shown in the diagram beneath.
Very nice displays of orbitals may be institute at the following sites:
J. Gutow, Univ. Wisconsin Oshkosh
R. Spinney, Ohio Land
M. Winter, Sheffield Academy

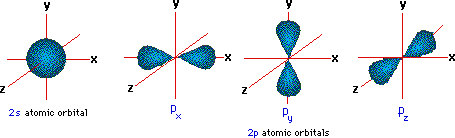
The valence beat out electron configuration of carbon is two_s ^two, 2p_x ¹, 2p_y ¹ & 2p_z ⁰. If this were the configuration used in covalent bonding, carbon would only be able to course two bonds. In this case, the valence shell would have six electrons- two shy of an octet. All the same, the tetrahedral structures of methane and carbon tetrachloride demonstrate that carbon can course iv equivalent bonds, leading to the desired octet. In order to explain this covalent bonding, Linus Pauling proposed an orbital hybridization model in which all the valence shell electrons of carbon are reorganized.

Hybrid Orbitals
In order to explain the structure of methane (CH₄), the 2s and three 2p orbitals are converted to four equivalent hybrid atomic orbitals, each having 25% s and 75% p character, and designated sp³. These hybrid orbitals accept a specific orientation, and the four are naturally oriented in a tetrahedral manner. Thus, the four covalent bonds of methane consist of shared electron pairs with four hydrogen atoms in a tetrahedral configuration, as predicted past VSEPR theory.

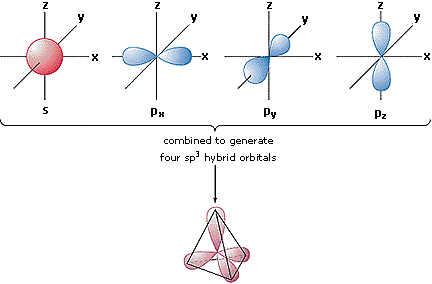
Molecular Orbitals
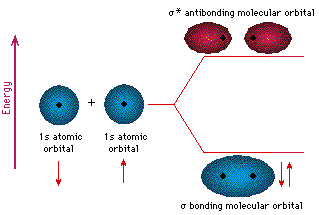
But every bit the valence electrons of atoms occupy atomic orbitals (AO), the shared electron pairs of covalently bonded atoms may be thought of as occupying molecular orbitals (MO). It is convenient to judge molecular orbitals by combining or mixing 2 or more than atomic orbitals. In general, this mixing of n atomic orbitals always generates n molecular orbitals. The hydrogen molecule provides a unproblematic example of MO formation. In the post-obit diagram, two 1s atomic orbitals combine to requite a sigma (σ) bonding (low energy) molecular orbital and a 2d higher energy MO referred to every bit an antibonding orbital. The bonding MO is occupied past two electrons of opposite spin, the event being a covalent bond.

The annotation used for molecular orbitals parallels that used for atomic orbitals. Thus, s-orbitals accept a spherical symmetry surrounding a single nucleus, whereas σ-orbitals have a cylindrical symmetry and embrace two (or more) nuclei. In the instance of bonds betwixt second period elements, p-orbitals or hybrid diminutive orbitals having p-orbital grapheme are used to form molecular orbitals. For example, the sigma molecular orbital that serves to bond two fluorine atoms together is generated past the overlap of p-orbitals (part A beneath), and two sp³ hybrid orbitals of carbon may combine to requite a similar sigma orbital. When these bonding orbitals are occupied by a pair of electrons, a covalent bond, the sigma bond results. Although we have ignored the remaining p-orbitals, their inclusion in a molecular orbital handling does not lead to any additional bonding, equally may be shown by activating the fluorine correlation diagram below.

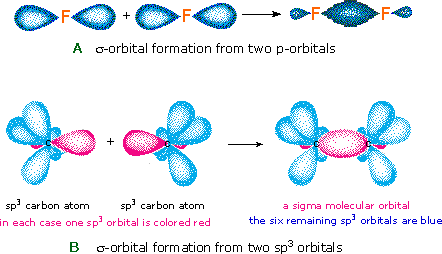
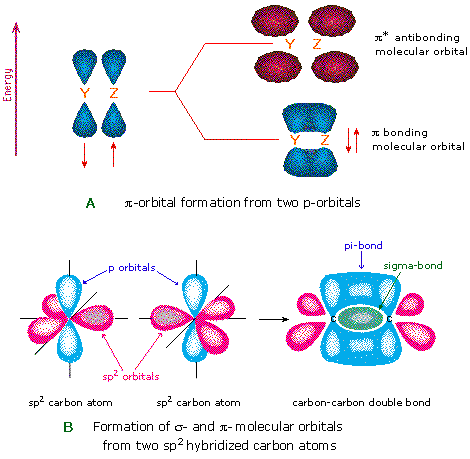
Another type of MO (the π orbital) may be formed from two p-orbitals by a lateral overlap, every bit shown in part A of the following diagram. Since bonds consisting of occupied π-orbitals (pi-bonds) are weaker than sigma bonds, pi-bonding between 2 atoms occurs only when a sigma bond has already been established. Thus, pi-bonding is generally found merely as a component of double and triple covalent bonds. Since carbon atoms involved in double bonds take only three bonding partners, they crave only three hybrid orbitals to contribute to iii sigma bonds. A mixing of the 2s-orbital with 2 of the 2p orbitals gives three sp² hybrid orbitals, leaving one of the p-orbitals unused. Two sp² hybridized carbon atoms are then joined together by sigma and pi-bonds (a double bail), as shown in part B.

The style in which atomic orbitals overlap to class molecular orbitals is really more than complex than the localized examples given higher up. These are useful models for explaining the construction and reactivity of many organic compounds, but modern molecular orbital theory involves the cosmos of an orbital correlation diagram. Two examples of such diagrams for the unproblematic diatomic elements F₂ and N₂ will be drawn above when the appropriate button is clicked. The 1s and 2s atomic orbitals do not provide any overall bonding, since orbital overlap is minimal, and the resulting sigma bonding and antibonding components would cancel. In both these cases three 2p diminutive orbitals combine to form a sigma and two pi-molecular orbitals, each as a bonding and antibonding pair. The overall bonding order depends on the number of antibonding orbitals that are occupied. The subtle alter in the energy of the σ_2p bonding orbital, relative to the two degenerate π-bonding orbitals, is due to due south-p hybridization that is unimportant to the present discussion.

One instance of the advantage offered past the molecular orbital approach to bonding is the oxygen molecule. Here, the correlation diagram correctly accounts for the paramagnetic character of this uncomplicated diatomic compound. As well, the orbital correlation diagram for methane provides another example of the difference in electron density predicted by molecular orbital calculations from that of the localized bond model. Click on the compound names for these displays.

A cartoon of the p and π orbitals of a double bond may exist examined by .

A model of the π orbitals of ethene may exist examined by .

The p-orbitals in these model are represented by crimson and bluish colored spheres or ellipses, which represent different phases, defined by the mathematical wave equations for such orbitals.

Finally, in the case of carbon atoms with only two bonding partners only ii hybrid orbitals are needed for the sigma bonds, and these sp hybrid orbitals are directed 180º from each other. Ii p-orbitals remain unused on each sp hybridized atom, and these overlap to give ii pi-bonds following the formation of a sigma bond (a triple bail), as shown below.

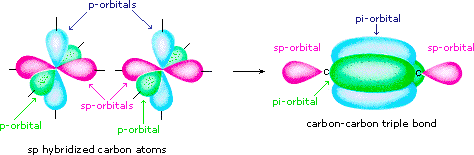
The various hybridization states of carbon may exist examined by .

Practice Issues

The following problems explore many of the concepts discussed to a higher place. They include recognition of dissimilar molecular shapes, obtaining structural information from molecular formulas, evaluation of line and condensed structural formulas, formal charges, hybridization and resonance.

Return to Table of Contents

This page is the property of William Reusch.   Comments, questions and errors should exist sent to whreusch@msu.edu.
These pages are provided to the IOCD to assist in capacity edifice in chemical education. 05/05/2013

wagnermadeelay42.blogspot.com

Source: https://www2.chemistry.msu.edu/faculty/reusch/VirtTxtJml/intro3.htm

Share this post